Best Paper Award at ICTAI 2024
Research of the Advanced Concepts Team was awarded with the Best Paper Award at the 36th IEEE International Conference on Tools with Artificial Intelligence (ICTAI) for contributions to the foundations of AI. The work establishes a powerful new framework in AI for addressing complex decision-making challenges that combines both cost and probabilistic reasoning. By introducing a flexible weighting scheme that simplifies and extends previous methodologies, this research provides a comprehensive foundation for advancements in probabilistic, cost-optimal reasoning.
Scientific Background
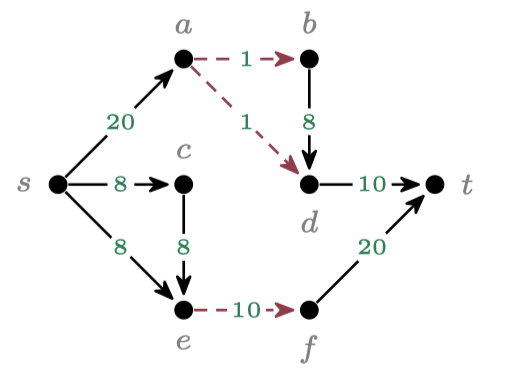
MaxSAT is the canonical problem of cost-optimal reasoning. It allows to compactly describe and solve optimization tasks such as the minimum cut problem: Given a graph with weights on the edges and two designated vertices s and t, the task is to select the cost-minimum number of edges to disconnect s and t. In the picture on the right, the optimal solution consists of the three red, dashed edges.
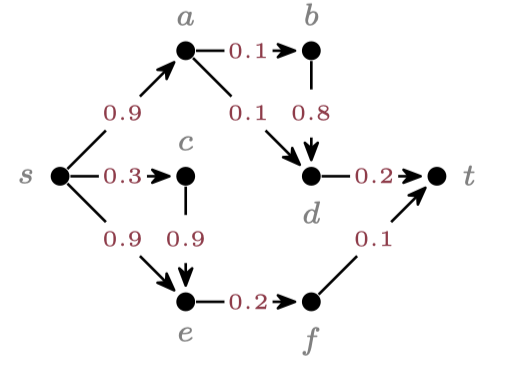
Projected model counting (#∃SAT), on the other hand, is the canonical problem of probabilistic reasoning. A typical question to be answered with this tool is: What is the probability that there is no path from s to t if edges fail with a certain probability? The same network from above is shown on the left with probabilities on the edges, and the probability that there is no s-t-path is 0.622. Adjacent research of the ACT uses projected model counting for instance to estimate the reliability of satellite constellations with inter-satellite links, which might exhibit failure with some probability due to factors like geography, weather conditions, hardware malfunctions, or positioning errors.

The natural extension of both approaches, which was studied in the awarded paper, is cost-optimal, probabilistic reasoning. For instance, in the minimum cut problem we may ask to select a cost-minimal number of edges to maximize the probability that s and t are disconnected. The image on the right shows an example instance with costs and probabilities on the edges. Combining both methodologies into one enables, for instance, an automatic optimization process of reliability constraints. A potential application in the future is the automatic design of reliable and robust satellite constellations.
Details of the Publication
Venue: 36th IEEE International Conference on Tools with Artificial Intelligence
Title: On Weighted Maximum Model Counting: Complexity and
Fragments
Authors: Max Bannach (ACT) and Markus Hecher (MIT)
Abstract:
Maximum model counting (MAX#∃SAT) is a recently introduced extension of projected model counting (#∃SAT) that maximizes over a set of variables X the number of assignments over a set Y that can be extended to a satisfying assignment over Z. It is known that MAX#∃SAT also generalizes weighted #∃SAT and MaxSAT if weights are introduced to the problem. However, for the latter a non-trivial gadget is needed. We propose a more generic weighting scheme that evaluates a fitness term and a probability term simultaneously. In this setting, MAX#∃SAT extends weighted MaxSAT and #∃ESAT without the need of gadgets. As MaxSAT is the canonical problem of cost-optimal reasoning and #∃SAT can be seen as canonical problem of probabilistic reasoning, MAX#∃SAT with the proposed weighting scheme naturally fills the role as canonical problem for cost-optimal probabilistic reasoning.
We study the problem from a complexity-theoretic point of view for unary weights and prove that the decision version is DP^P_2-complete. We then focus on structural parameters and provide an ETH lower bound with respect to the inputs treewidth, as well as a treewidth-aware reduction from MAX#∃SAT to MAX#SAT.