Geodesy of irregular small bodies via neural density fields: geodesyNets
The general problem of determining the density distribution of celestial bodies and induced gravitational pull is of great importance in numerous situations such as performing orbital and surface proximity operations. Knowledge of the density distribution can also provide insight on the body's origin and composition. Measuring the gravitational pull or observing object trajectories can provide data to match a predicted gravitational field to observations. In practice, the state-of-the-art approaches for modelling the gravity field are spherical harmonics, mascon models and polyhedral gravity. All of these, however, introduce some requirements such as knowledge of precise shape model or assume homogeneous internal density. geodesyNets are able to compete with these approaches without many of the requirements. Additionally, they are able to model hetergeneous density fields. Further, we have successfully applied it to data from real observed trajectory data to validate the viability of the approach.
Project overview
geodesyNets are inspired by recent advances in 3D scene reconstruction made by Mildenhall et al. [1] where they solve the inverse problem of predicting images of objects from unseen angles. A geodesyNet, however, is tasked with predicting the density of a body at a given coordinate. From these densities, we can numerically approximate the gravitational pull on an object by sampling the geodesyNet at a large number of points. Comparing to actually experienced accelerations caused by the real body (or a model of it) allows training the geodesyNet.

With geodesyNets we are able to accurately reconstruct what we refer to as the neural density field of homogeneous bodies. This is depicted in Figure 2. Note that these results do not rely on any shape information or assumptions like a homogeneous density profile. The network itself learns to represent it homogeneously.

Similarly, as seen in Figure 2, we show that we are able to reconstruct the neural density field of heterogeneous bodies with even better precision if we rely on shape information about the investigated body.
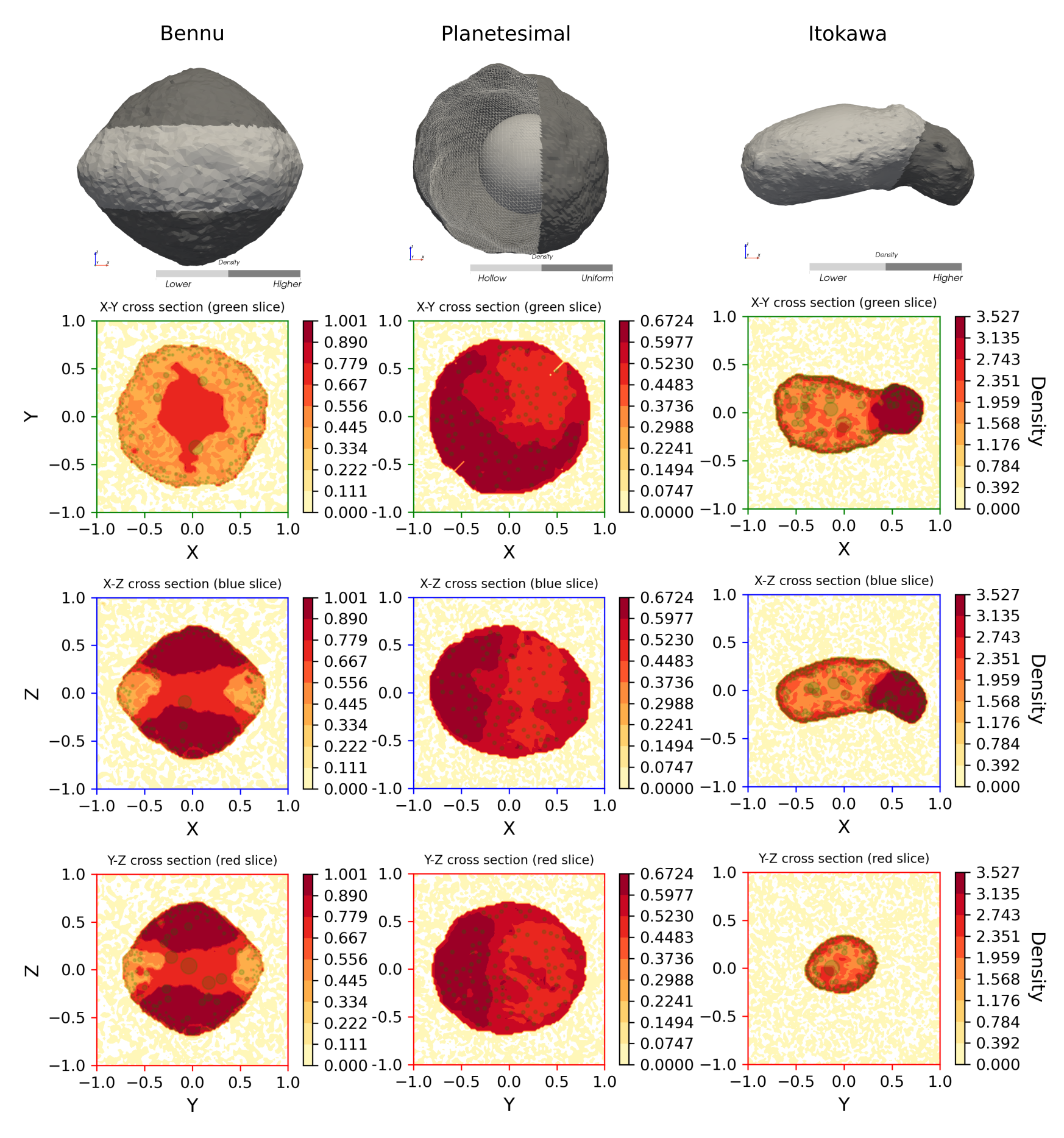
Building on these successes we have now moved to investigating applications with real experimental data. Code for this project can be found online.
References:
Mildenhall, B., Srinivasan, P.P., Tancik, M., Barron, J.T., Ramamoorthi, R. and Ng, R., 2020, August. Nerf: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision (pp. 405-421). Springer, Cham.
Izzo, D. and Gómez, P., 2021. Geodesy of irregular small bodies via neural density fields: geodesyNets. arXiv preprint arXiv:2105.13031.