Neural Kepler Map

Background

Keplerian motion has long been a building block for mission analysts, but low-energy missions often require more accurate dynamical models that account for the gravitational influence of multiple bodies. Designing optimal trajectories within such frameworks remains a significant challenge.

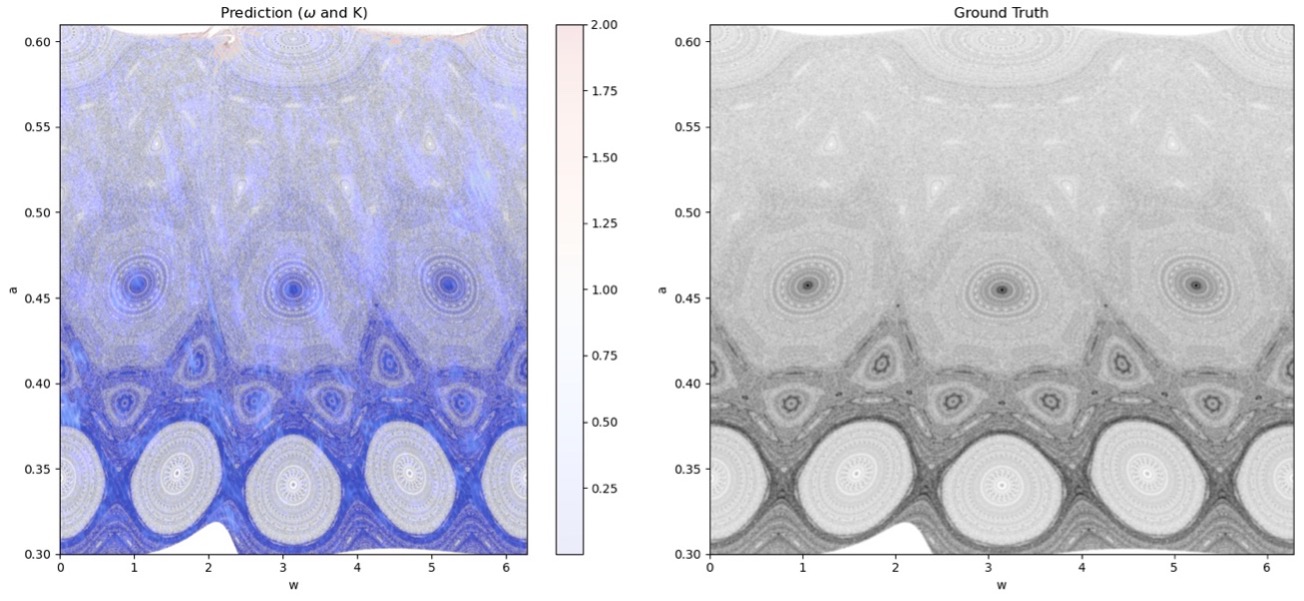
Project

One promising approach to tackle this complexity, reducing its dimensionality, involves the use of Poincaré maps at surfaces of section corresponding to periapsis passages of the perturbed trajectories[1,2]. These maps enable the development of a simplified analytical model, known as the Keplerian map[3], to describe the sequence of periapsis passages and analyze long-term trajectory evolution. While this approach facilitates trajectory design and offers valuable insights, its low accuracy forbids its use in scenarios where third-body perturbations are substantial, such as in cis-lunar space. In this study, we address this limitation by replacing the classical analytical Keplerian map with a novel and more general neural network model, trained to accurately reproduce the map in the planar circular restricted three-body problem while not being subject to previous limitations. Our results enable the generalization of Keplerian maps to highly perturbed dynamical environments.

References

[1] T.Y. Petrosky, R. Brouke, “Area-preserving mappings and deterministic chaos for nearly parabolic motions”, Celestial Mechanics 42, 53–79 (1987).

[2] Ivan I. Shevchenko. “The Kepler map in the three-body problem”, New Astronomy 16(2), 94-99 (2011).

[3] Shane D. Ross, Daniel J. Scheeres, “Multiple Gravity Assists, Capture, and Escape in the Restricted Three-Body Problem”, SIAM Journal on Applied Dynamical Systems 6(3), 576-596 (2007).